coordinated grid system to determine location on Earth. From the chapter’s opening photograph, you can see the importance of determining the location of the research ship and tracking the locations of tabular icebergs. The terms latitude and longitude were in use on maps as early as the first century A.D., with the concepts themselves dating back to Eratosthenes and others.
The geographer, astronomer, and mathematician Ptolemy (ca. A.D. 90–168) contributed greatly to the development of modern maps, and many of his terms are still used today. Ptolemy divided the circle into 360 degrees (360°), with each degree having 60 minutes (60′) and each minute having 60 seconds (600) in a manner adapted from the ancient Babylonians. He located places using these degrees, minutes, and seconds. However, the precise length of a degree of latitude and a degree of longitude remained unresolved for the next 17 centuries.
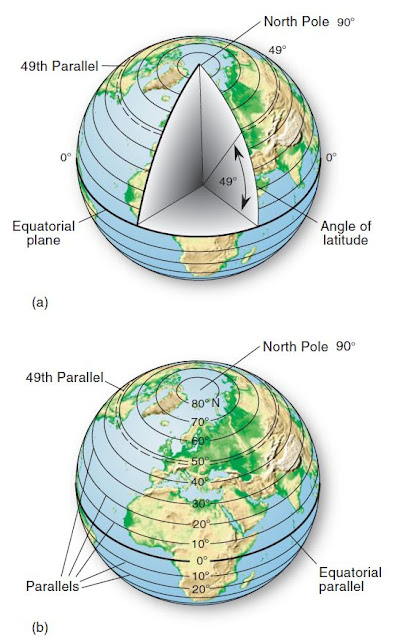
Latitude is an angular distance north or south of the equator, measured from the center of Earth (Figure). On a map or globe, the lines designating these angles of latitude run east and west, parallel to the equator (Figure). Because Earth’s equator divides the distance between the North Pole and the South Pole exactly in half, it is assigned the value of 0° latitude. Thus, latitude increases from the equator northward to the North Pole, at 90° N latitude, and southward to the South Pole, at 90° S latitude.
A line connecting all points along the same latitudinal angle is a parallel. In the figure, an angle of 49° N latitude is measured, and, by connecting all points at this latitude, we have the 49th parallel. Thus, latitude is the name of the angle (49° N latitude), parallel names the line (49th parallel), and both indicate distance north of the equator.
Latitude is readily determined by observing fixed celestial objects such as the Sun or the stars, a method dating to ancient times. During daylight hours, the angle of the Sun above the horizon indicates the observer’s latitude, after adjustment is made for the season and for the time of day. Because Polaris (the North Star) is almost directly overhead at the North Pole, persons anywhere in the Northern
Hemisphere can determine their latitude at night simply by sighting Polaris and measuring its angle above the local horizon. The angle of elevation of Polaris above the horizon indicates the latitude of the observation point. Go to this chapter on our Mastering Geography web site to see an illustration of sighting on Polaris to determine latitude. In the Southern Hemisphere, Polaris cannot be seen because it is below the horizon. Instead, latitude south of the equator is measured by sighting on a constellation that points to a celestial location above the South Pole. This indicator constellation is the Southern Cross (Crux Australis).
The geographer, astronomer, and mathematician Ptolemy (ca. A.D. 90–168) contributed greatly to the development of modern maps, and many of his terms are still used today. Ptolemy divided the circle into 360 degrees (360°), with each degree having 60 minutes (60′) and each minute having 60 seconds (600) in a manner adapted from the ancient Babylonians. He located places using these degrees, minutes, and seconds. However, the precise length of a degree of latitude and a degree of longitude remained unresolved for the next 17 centuries.
Latitude
Latitude is an angular distance north or south of the equator, measured from the center of Earth (Figure). On a map or globe, the lines designating these angles of latitude run east and west, parallel to the equator (Figure). Because Earth’s equator divides the distance between the North Pole and the South Pole exactly in half, it is assigned the value of 0° latitude. Thus, latitude increases from the equator northward to the North Pole, at 90° N latitude, and southward to the South Pole, at 90° S latitude. A line connecting all points along the same latitudinal angle is a parallel. In the figure, an angle of 49° N latitude is measured, and, by connecting all points at this latitude, we have the 49th parallel. Thus, latitude is the name of the angle (49° N latitude), parallel names the line (49th parallel), and both indicate distance north of the equator.
Latitude is readily determined by observing fixed celestial objects such as the Sun or the stars, a method dating to ancient times. During daylight hours, the angle of the Sun above the horizon indicates the observer’s latitude, after adjustment is made for the season and for the time of day. Because Polaris (the North Star) is almost directly overhead at the North Pole, persons anywhere in the Northern
Hemisphere can determine their latitude at night simply by sighting Polaris and measuring its angle above the local horizon. The angle of elevation of Polaris above the horizon indicates the latitude of the observation point. Go to this chapter on our Mastering Geography web site to see an illustration of sighting on Polaris to determine latitude. In the Southern Hemisphere, Polaris cannot be seen because it is below the horizon. Instead, latitude south of the equator is measured by sighting on a constellation that points to a celestial location above the South Pole. This indicator constellation is the Southern Cross (Crux Australis).
Latitudinal Geographic Zones
Natural environments differ dramatically from the equator to the poles. These differences result from the amount of solar energy received, which varies by latitude and season of the year. As a convenience, geographers identify latitudinal geographic zones as regions. “Lower latitudes” are those nearer the equator, whereas “higher latitudes” are those nearer the poles. Figure portrays these zones, their locations, and their names: equatorial and tropical, subtropical, midlatitude, subarctic or subantarctic, and arctic or antarctic. These generalized latitudinal zones are useful for reference and comparison, but they do not have rigid boundaries; rather, think of them as transitioning one to another.
The Tropic of Cancer (about 23.5° N parallel) and the Tropic of Capricorn (about 23.5° S parallel) are the most extreme northern and southern parallels that experience perpendicular (directly overhead) rays of the Sun at local noon. When the Sun arrives overhead at these tropics, it marks the first day of summer in each hemisphere. (Further discussion of the tropics is in Chapter 2.) The Arctic Circle (about 66.5° N parallel) and the Antarctic Circle (about 66.5° S parallel) are the parallels farthest
from the poles that still experience 24 uninterrupted hours of night (including dawn and twilight) during local winter or continuous day during local summer.
Longitude
Longitude is an angular distance east or west of a point on Earth’s surface, measured from the center of Earth (Figure). On a map or globe, the lines designating these angles of longitude run north and south (Figure). A line connecting all points along the same longitude is a meridian. In the figure, a longitudinal angle of 60° E is measured. These meridians run at right angles (90°) to all parallels, including the equator.
Thus, longitude is the name of the angle, meridian names the line, and both indicate distance east or west of an arbitrary prime meridian a meridian designated as 0° (Figure). Earth’s prime meridian passes through the old Royal Observatory at Greenwich, England, as set by an 1884 treaty—the Greenwich prime meridian.
Determination of Latitude and Longitude
Table compares the length of latitude and longitude degrees. Because meridians of longitude converge toward the poles, the actual distance on the ground spanned by a degree of longitude is greatest at the equator (where meridians separate to their widest distance apart) and diminishes to zero at the poles (where meridians converge). In comparison, note the consistent distance represented by a degree of latitude from equator to poles. For your latitude degree and longitude degree, find the nearest linear value for each.
We noted that latitude is determined easily by sighting the Sun or the North Star or by using the Southern Cross as a pointer. In contrast, a method of accurately determining longitude, especially at sea, remained a major difficulty in navigation until after 1760. The key to measuring the longitude of a place lies in accurately knowing time.